There’s an equation that gives many people pause:
8 ÷ 2(2 + 2)
What is the answer here?
Is there a correct answer?
Yes. Or perhaps… it depends.
Yes, there is a correct answer from an engineer’s or a mathematician’s perspective. Everything within parentheses has to be manipulated before everyone else. That is, everything contained in parentheses has to be considered before understanding what comes next. The brackets have to be eliminated by manipulating the expression within the brackets.
2+2 = 4
Now what?
According to the rules of arithmetic, in any kind of expression one proceeds in order: first with division, then multiplication, then addition, then subtraction, what some people abbreviate as PODMAS or BODMAS to symbolize parentheses/brackets, outside, division, multiplication, addition, subtraction.
What is within the parentheses/brackets has been solved and with the parentheses/brackets eliminated, engineers and mathematicians would rewrite the equation as such: 8 ÷ 2(2 + 2). And follow the order above, with division before multiplication. 4 x 4 = 16.
However, BODMAS is not a universally accepted routine. In other countries, POMDAS (not PODMAS) is used, where multiplication comes first. The argument is with division and multiplication. It seems that in every country mathematicians or arithmeticians have accepted that addition and subtraction are simply not the same, and they seem to have largely accepted that addition must precede subtraction in any given routine. Not so with division and multiplication. Mathematicians are divided on whether these are the same or different.
The expression above, 8 ÷ 2(2 + 2), is readily rendered without trouble as, 8 ÷ 2 x 4. Which is where trouble begins. Depending on whether you proceed with the manipulation with the routine PODMAS or POMDAS, the result will reveal one’s country of mathematics education, or even one’s basic philosophy.
National or personal mathematical philosophies aside, the way the original expression is written is unclear, confusing, or easily misinterpreted. But of course, that is probably the point of the exercise. To test a philosophical idea, one must subject it to its margins of confusion. The expression 8 ÷ 2(2 + 2) tests the will of mathematical rule making, rule building and maintenance. It tests the will of an algorithm.
Philosophy and algorithms aside, can common sense prevail? Consider this other thought: One might easily re-write and interpret the equation 8 ÷ 2(2 + 2) easily as 8/2(2+2), which more intuitively can be imagined simply as:
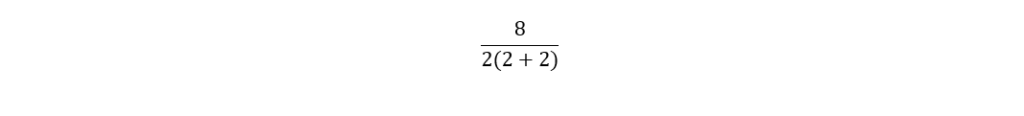
…in which case the value is = 1, which is the same value one would expect using the POMDAS routine.
Common sense here agrees with the POMDAS routine. That is not to say that this result always occurs. In fact, it is the very failure of common sense in complex and complicated analysis that gave rise to the use and adoption of mathematical routines, the adoption of algorithms. To put this another way, common sense is not always correct!
So, what is the answer to the equation, you may ask? Some people might say 16 and others 1.
Is there a correct answer?
To get to the heart of this question, one must resolve the conundrums that arise: one must explore and critique the inherent philosophies at stake.
Are division and multiplication essentially the same? Why do mathematicians accept that addition and subtraction are different yet seem to imply that division and multiplication are the same?
In other words, is to divide quantity by 2 the same as to multiply the same quantity by 0.5 Are these the same expression or different expressions, and if the latter, by how much do they differ?
Though in some cases, they may lead to the same result, they are different and much be treated as such.
Do you go with the rule or with your gut, if in fact the two provide different responses?
What is the strictest application of the rules of mathematical manipulation compared to what makes intuitive sense?
Is the law always right or do instances exist where intuition makes for the better guide?
If we are to judge how many of one hundred people choose 16 or 1, and our enjoyment of life dependent upon our making the correct prediction, which number would be the optimal answer? How many of those one hundred people are engineers or mathematics or people who have had formal training in answering these questions using the proper procedures? On the other hand, if we are to write an examination and answering this question correctly would give us prized admission to a noble intellectual society, it is not by coincidence that the same question might present a different ideal answer—or at least an additional challenge.
What this equation shows, more than whether one’s computational skills are apt, is that what matters more than any question or answer being inherently correct or incorrect are the context and the audience—the environment in which the puzzle is embedded and the ultimate recipient of the response.
What is the situation, who is listening, who is interested in the response, and what is at stake governs our thought process, our reasoning, and our evaluation. Needless to say, even mathematics in laden with bias. The simplest of equations can elucidate pervasive subjectivity even in those subjects most assumed to be pure and objective. Solving an equation is about knowing the rules or the formulas but also sorely important is knowing the people setting the questions and their hidden intentions.

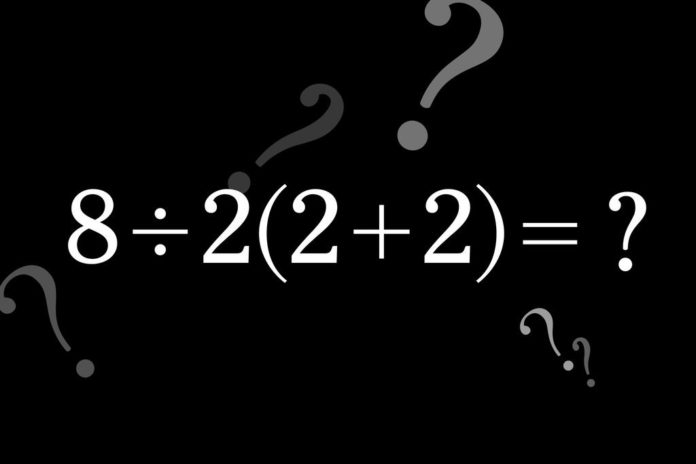









In the above illustration whether you approach 8/2*4 by (BODMAS/PODMAS) or (POMDAS) you’ll still arrive at the same answer which is 16; in POMDAS you could rephrase it as 4*8/2 and in this way start with multiplication fast.
There is no doubt that the universe is governed by certain mathematical rules. It is our limited or partial knowledge of these rules that brings about biases as opposed to mathematics itself. It is these rules that have been gradually (re)discovered applied in the fields such as quantum physics to usher in the new technological age of electronics that sparked off in the last century. In the same vein, advanced mathematical rules were used in the building of the pyramids in ancient Egypt and Kush; and to this day, 5000 years later, the pyramids still hold.
In essence, the mathematical rules abound in the universe have been with us for a long time and even precede us; we are only beginning to discover these rules that perhaps form the basis of the existence of both the universe and that of living beings. In deed, as some scientist have noted the ultimate question on the origins of the existence of our universe is coming round to whether mathematical rules emanated at the birth of the universe or it have always existed independent of the universe.
Coincidentally the speculations being drawn out by modern scientific inquiry on the role of mathematics in creation takes us back full circle to what ancient Egyptians called neteru (nature); meaning the principles that created the universe and brought forth the natural forces which were later to acquire religious significance as “gods” (of thunder, storm, sky, sea etc) and subsequently gained political significance as rulers became sons of these gods for purposes of political clout and social mass control.
Remarkably, ancient Egyptians had already seen conceptualized god as a set of principles that governed the universe and presently scientists are informed by similar thinking when they go in search of the so called “god particles”. Both ideas seem to lean towards a somewhat mathematical god as opposed to a man god.
Interesting theories here, Mkuki. If only we could connect back to human history more in everyday life so that we do not miss these points of overlap and could actually move forward in our knowlege of the universe.